Excel财务函数用法大全! 干货! 强烈建议收藏!
EXCEL 提供了许多财务函数,这些函数大体上可分为四类:投资计算函数、折旧计算函数、偿还率计算函数、债券及其他金融函数。这些函数为财务分析提供了极大的便利。利用这些函数,可以进行一般的财务计算,如确定贷款的支付额、投资的未来值或净现值,以及债券或息票的价值等等。
使用这些函数不必理解高级财务知识,只要填写变量值就可以了。 下面给出了财务函数列表。
( 1 ) 投资计算函数| 函数名称 | 函 数功 能 |
| EFFECT | 计算实际年利息率 |
| FV | 计算投资的未来值 |
| FVSCHEDULE | 计算原始本金经一系列复利率计算之后的未来值 |
| IPMT | 计算某投资在给定期间内的支付利息 |
| NOMINAL | 计算名义年利率 |
| NPER | 计算投资的周期数 |
| NPV | 在已知定期现金流量和贴现率的条件下计算某项投资的净现值 |
| PMT | 计算某项年金每期支付金额 |
| PPMT | 计算某项投资在给定期间里应支付的本金金额 |
| PV | 计算某项投资的净现值 |
| XIRR | 计算某一组不定期现金流量的内部报酬率 |
| XNPV | 计算某一组不定期现金流量的净现值 |
( 2 ) 折旧计算函数
| 函数名称 | 函 数功 能 |
| AMORDEGRC | 计算每个会计期间的折旧值 |
| DB | 计算用固定定率递减法得出的指定期间内资产折旧值 |
| DDB | 计算用双倍余额递减或其它方法得出的指定期间内资产折旧值 |
| SLN | 计算一个期间内某项资产的直线折旧值 |
| SYD | 计算一个指定期间内某项资产按年数合计法计算的折旧值 |
| VDB | 计算用余额递减法得出的指定或部分期间内的资产折旧值 |
( 3 ) 偿还率计算函数
| 函数名称 | 函 数功 能 |
| IRR | 计算某一连续现金流量的内部报酬率 |
| MIRR | 计算内部报酬率。此外正、负现金流量以不同利率供给资金计算 |
| RATE | 计算某项年金每个期间的利率 |
( 4 ) 债券及其他金融函数
| 函数名称 | 函 数功 能 |
| ACCRINTM | 计算到期付息证券的应计利息 |
| COUPDAYB | 计算从付息期间开始到结算日期的天数 |
| COUPDAYS | 计算包括结算日期的付息期间的天数 |
| COUPDAYSNC | 计算从结算日期到下一个付息日期的天数 |
| COUPNCD | 计算结算日期后的下一个付息日期 |
| COUPNUM | 计算从结算日期至到期日期之间的可支付息票数 |
| COUPPCD | 计算结算日期前的上一个付息日期 |
| CUMIPMT | 计算两期之间所支付的累计利息 |
| CUMPRINC | 计算两期之间偿还的累计本金 |
| DISC | 计算证券的贴现率 |
| DOLLARDE | 转换分数形式表示的货币为十进制表示的数值 |
| DOLLARFR | 转换十进制形式表示的货币分数表示的数值 |
| DURATION | 计算定期付息证券的收现平均期间 |
| INTRATE | 计算定期付息证券的利率 |
| ODDFPRICE | 计算第一个不完整期间面值 $100 的证券价格 |
| ODDFYIELD | 计算第一个不完整期间证券的收益率 |
| ODDLPRICE | 计算最后一个不完整期间面值 $100 的证券价格 |
| ODDLYIELD | 计算最后一个不完整期间证券的收益率 |
| PRICE | 计算面值 $100 定期付息证券的单价 |
| PRICEDISC | 计算面值 $100 的贴现证券的单价 |
| PRICEMAT | 计算面值 $100 的到期付息证券的单价 |
| PECEIVED | 计算全投资证券到期时可收回的金额 |
| TBILLPRICE | 计算面值 $100 的国库债券的单价 |
| TBILLYIELD | 计算国库债券的收益率 |
| YIELD | 计算定期付息证券的收益率 |
| YIELDDISC | 计算贴现证券的年收益额 |
| YIELDMAT | 计算到期付息证券的年收益率 |
在财务函数中有两个常用的变量: f 和 b, 其中 f 为年付息次数,如果按年支付,则 f=1 ;按半年期支付,则 f=2 ;按季支付,则 f=4 。 b 为日计数基准类型,如果日计数基准为 “US ( NASD ) 30/360” ,则 b=0 或省略;如果日计数基准为 “ 实际天数 / 实际天数 ” ,则 b=1 ;如果日计数基准为 “ 实际天数 /360” ,则 b=2 ;如果日计数基准为 “ 实际天数 /365” ,则 b=3 如果日计数基准为 “ 欧洲 30/360” ,则 b=4 。
下面介绍一些常用的财务函数。
1 . ACCRINT( is, fs, s, r,p,f,b) 该函数返回定期付息有价证券的应计利息。其中 is 为有价证券的发行日, fs 为有价证券的起息日, s 为有价证券的成交日,即在发行日之后,有价证券卖给购买者的日期, r 为有价证券的年息票利率, p 为有价证券的票面价值,如果省略 p ,函数 ACCRINT 就会自动将 p 设置为¥ 1000 , f 为年付息次数, b 为日计数基准类型。 例如 ,某国库券的交易情况为:发行日为 95 年 1 月 31 日 ;起息日为 95 年 7 月 30 日 ;成交日为 95 年 5 月 1 日 ,息票利率为 8.0% ;票面价值为¥ 3,000 ;按半年期付息;日计数基准为 30/360 ,那么应计利息为: =ACCRINT("95/1/31","95/7/30","95/5/1",0.08,3000,2,0) 计算结果为: 60.6667 。 2. ACCRINTM(is, m,r, p, b) 该函数返回到期一次性付息有价证券的应计利息。其中 i 为有价证券的发行日, m 为有价证券的到期日, r 为有价证券的年息票利率, p 为有价证券的票面价值,如果省略 p , 函数 ACCRINTM 就会自动将 p 为¥ 1000 , b 为日计数基准类型。 例如 ,一个短期债券的交易情况如下:发行日为 95 年 5 月 1 日 ;到期日为 95 年 7 月 18 日 ;息票利息为 9.0% ;票面价值为¥ 1,000 ;日计数基准为实际天数 /365 。那么应计利息为: =ACCRINTM("95/5/1","95/7/18",0.09,1000,3) 计算结果为: 19.23228 。 3 . CUMPRINC ( r,np,pv,st,en,t ) 该函数返回一笔货款在给定的 st 到 en 期间累计偿还的本金数额。其中 r 为利率, np 为总付款期数, pv 为现值, st 为计算中的首期,付款期数从 1 开始计数, en 为计算中的末期, t 为付款时间类型,如果为期末,则 t=0 ,如果为期初,则 t=1 。 例如 ,一笔住房抵押贷款的交易情况如下:年利率为 9.00% ;期限为 25 年;现值为¥ 110 , 000 。由上述已知条件可以计算出: r=9.00%/12=0.0075 , np=30*12=360 。那么该笔贷款在第下半年偿还的全部本金之中(第 7 期到第 12 期)为: CUMPRINC(0.0075,360,110000,7,12,0) 计算结果为: -384.180 。 该笔贷款在第一个月偿还的本金为: =CUMPRINC(0.0075,360,110000,1,1,0) 计算结果为: -60.0849 。 4 . DISC ( s,m,pr,r,b ) 该函数返回有价证券的贴现率。其中 s 为有价证券的成交日,即在发行日之后,有价证券卖给购买者的日期, m 为有价证券的到日期,到期日是有价证券有效期截止时的日期, pr 为面值为 “ ¥ 100” 的有价证券的价格, r 为面值为 “ ¥ 100” 的有价证券的清偿价格, b 为日计数基准类型。 例如 :某债券的交易情况如下:成交日为 95 年 3 月 18 日 ,到期日为 95 年 8 月 7 日 ,价格为¥ 45.834 ,清偿价格为¥ 48 ,日计数基准为实际天数 /360 。那么该债券的贴现率为: DISC("95/3/18","95/8/7",45.834,48,2) 计算结果为: 0.114401 。5 . EFFECT ( nr , np )
该函数利用给定的名义年利率和一年中的复利期次,计算实际年利率。其中 nr 为名义利率, np 为每年的复利期数。 例如 : EFFECT ( 6.13%,4 )的计算结果为 0.062724 或 6.2724% 6. FV(r,np,p,pv,t) 该函数基于固定利率及等额分期付款方式,返回某项投资的未来值。其中 r 为各期利率,是一固定值, np 为总投资(或贷款)期,即该项投资(或贷款)的付款期总数, p 为各期所应付给(或得到)的金额,其数值在整个年金期间(或投资期内)保持不变,通常 P 包括本金和利息,但不包括其它费用及税款, pv 为现值,或一系列未来付款当前值的累积和,也称为本金,如果省略 pv ,则假设其值为零, t 为数字 0 或 1 ,用以指定各期的付款时间是在期初还是期末,如果省略 t ,则假设其值为零。 例如 : FV ( 0.6%,12,-200,-500,1 )的计算结果为¥ 3,032.90 ; FV(0.9%,10,-1000) 的计算结果为¥ 10,414.87 ; FV(11.5%/12,30,-2000,,1) 的计算结果为¥ 69,796.52 。 又如 ,假设需要为一年后的一项工程预筹资金,现在将¥ 2000 以年利 4.5% ,按月计息(月利为 4.5%/12 )存入储蓄存款帐户中,并在以后十二个月的每个月初存入¥ 200 。那么一年后该帐户的存款额为: FV(4.5%/12, 12,-200,-2000,1) 计算结果为¥ 4,551.19 。 7 . FVSCHEDULE ( p,s ) 该函数基于一系列复利返回本金的未来值,它用于计算某项投资在变动或可调利率下的未来值。其中 p 为现值, s 为利率数组。 例如 : FVSCHEDULE ( 1,{0.08,0.11,0.1} )的计算结果为 1.31868 。8 . IRR ( v,g )
该函数返回由数值代表的一组现金流的内部收益率。这些现金流不一定必须为均衡的,但作为年金,它们必须按固定的间隔发生,如按月或按年。内部收益率为投资的回收利率,其中包含定期支付(负值)和收入(正值)。其中 v 为数组或单元格的引用,包含用来计算内部收益率的数字, v 必须包含至少一个正值和一个负值,以计算内部收益率,函数 IRR 根据数值的顺序来解释现金流的顺序,故应确定按需要的顺序输入了支付和收入的数值,如果数组或引用包含文本、逻辑值或空白单元格,这些数值将被忽略; g 为对函数 IRR 计算结果的估计值, excel 使用迭代法计算函数 IRR 从 g 开始,函数 IRR 不断修正收益率,直至结果的精度达到 0.00001% ,如果函数 IRR 经过 20 次迭代,仍未找到结果,则返回错误值 #NUM !,在大多数情况下,并不需要为函数 IRR 的计算提供 g 值,如果省略 g ,假设它为 0.1 ( 10% )。如果函数 IRR 返回错误值 #NUM !,或结果没有靠近期望值,可以给 g 换一个值再试一下。 例如 ,如果要开办一家服装商店,预计投资为¥ 110,000 ,并预期为今后五年的净收益为:¥ 15,000 、¥ 21,000 、¥ 28,000 、¥ 36,000 和¥ 45,000 。 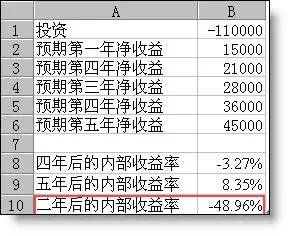
9 . NPV(r,v1,v2,...)
该函数基于一系列现金流和固定的各期贴现率,返回一项投资的净现值。投资的净现值是指未来各期支出(负值)和收入(正值)的当前值的总和。其中, r 为各期贴现率,是一固定值; v1,v2,... 代表 1 到 29 笔支出及收入的参数值, v1,v2,... 所属各期间的长度必须相等,而且支付及收入的时间都发生在期末, NPV 按次序使用 v1,v2 ,来注释现金流的次序。所以一定要保证支出和收入的数额按正确的顺序输入。如果参数是数值、空白单元格、逻辑值或表示数值的文字表示式,则都会计算在内;如果参数是错误值或不能转化为数值的文字,则被忽略,如果参数是一个数组或引用,只有其中的数值部分计算在内。忽略数组或引用中的空白单元格、逻辑值、文字及错误值。 例如 ,假设第一年投资¥ 8,000 ,而未来三年中各年的收入分别为¥ 2,000 ,¥ 3,300 和¥ 5,100 。假定每年的贴现率是 10% ,则投资的净现值是: NPV(10%,-8000,2000,3300,5800) 计算结果为:¥ 8208.98 。该例中,将开始投资的¥ 8,000 作为 v 参数的一部分,这是因为付款发生在第一期的期末。( “ 函数 .xls” 文件) 下面考虑在第一个周期的期初投资的计算方式。又如,假设要购买一家书店,投资成本为¥ 80,000 ,并且希望前五年的营业收入如下:¥ 16,000 ,¥ 18, 000 ,¥ 22,000 ,¥ 25,000 ,和¥ 30,000 。每年的贴现率为 8% (相当于通贷膨胀率或竞争投资的利率),如果书店的成本及收入分别存储在 B1 到 B6 中,下面的公式可以计算出书店投资的净现值: NPV ( 8%,B2:B6 ) +B1 计算结果为:¥ 6,504.47 。在该例中,一开始投资的¥ 80,000 并不包含在 v 参数中,因为此项付款发生在第一期的期初。 假设该书店的营业到第六年时,要重新装修门面,估计要付出¥ 11,000 ,则六年后书店投资的净现值为: NPV ( 8%,B2:B6,-15000 ) +B1 计算结果为: - ¥ 2,948.0810 . PMT ( r,np,p,f,t )
该函数基于固定利率及等额分期付款方式,返回投资或贷款的每期付款额。其中, r 为各期利率,是一固定值, np 为总投资(或贷款)期,即该项投资(或贷款)的付款期总数, pv 为现值,或一系列未来付款当前值的累积和,也称为本金, fv 为未来值,或在最后一次付款后希望得到的现金余额,如果省略 fv ,则假设其值为零(例如,一笔贷款的未来值即为零), t 为 0 或 1 ,用以指定各期的付款时间是在期初还是期末。如果省略 t ,则假设其值为零。 例如 ,需要 10 个月付清的年利率为 8% 的¥ 10,000 贷款的月支额为: PMT ( 8%/12,10,10000 ) 计算结果为: - ¥ 1,037.03 。 又如 ,对于同一笔贷款,如果支付期限在每期的期初,支付额应为: PMT ( 8%/12,10,10000,0,1 ) 计算结果为: - ¥ 1,030.16 。 再如 :如果以 12% 的利率贷出¥ 5,000 ,并希望对方在 5 个月内还清,那么每月所得款数为: PMT ( 12%/12,5,-5000 ) 计算结果为:¥ 1,030.20 。11 . PV ( r,n,p,fv,t )
计算某项投资的现值。年金现值就是未来各期年金现在的价值的总和。如果投资回收的当前价值大于投资的价值,则这项投资是有收益的。 例如 ,借入方的借入款即为贷出方贷款的现值。其中 r ( rage )为各期利率。 如果按 10% 的年利率借入一笔贷款来购买住房,并按月偿还贷款,则月利率为 10%/12 (即 0.83% )。可以在公式中输入 10%/12 、 0.83% 或 0.0083 作为 r 的值; n ( nper )为总投资(或贷款)期,即该项投资(或贷款)的付款期总数。对于一笔 4 年期按月偿还的住房贷款,共有 4*12 (即 48 )个偿还期次。可以在公式中输入 48 作为 n 的值; p ( pmt )为各期所应付给(或得到)的金额,其数值在整个年金期间(或投资期内)保持不变,通常 p 包括本金和利息,但不包括其他费用及税款。例如,¥ 10 , 000 的年利率为 12% 的四年期住房贷款的月偿还额为¥ 263.33 ,可以在公式中输入 263.33 作为 p 的值; fv 为未来值,或在最后一次支付后希望得到的现金余额,如果省略 fv ,则假设其值为零(一笔贷款的未来值即为零)。 例如 ,如果需要在 18 年后支付¥ 50,000 ,则 50,000 就是未来值。可以根据保守估计的利率来决定每月的存款额; t ( type )为数字 0 或 1 ,用以指定各期的付款时间是在期初还是期末,如果省略 t ,则假设其值为零。 例如 ,假设要购买一项保险年金,该保险可以在今后二十年内于每月末回报¥ 500 。此项年金的购买成本为 60,000 ,假定投资回报率为 8% 。那么该项年金的现值为: PV(0.08/12, 12*20,500,,0) 计算结果为: - ¥ 59,777.15 。负值表示这是一笔付款,也就是支出现金流。年金(¥ 59 , 777.15 )的现值小于实际支付的(¥ 60,000 )。因此,这不是一项合算的投资。 在计算中要注意优质 t 和 n 所使用单位的致性。 12 . SLN ( c,s,l )该函数返回一项资产每期的直线折旧费。其中 c 为资产原值, s 为资产在折旧期末的价值(也称为资产残值), 1 为折旧期限(有时也称作资产的生命周期)。 例如 ,假设购买了一辆价值¥ 30,000 的卡车,其折旧年限为 10 年,残值为¥ 7,500 ,那么每年的折旧额为: SLN ( 30000,7500,10 ) 计算结果为:¥ 2,250 。
(职场责编:拓荒牛
 )
)

 晋ICP备17002471号-6
晋ICP备17002471号-6